Evolving scientific discovery by unifying data and background knowledge with AI Hilbert

We next state the main theoretical results that underpin AI-Hilbert and describe the methods used to address the problems studied to validate AI-Hilbert.

Preliminaries

We let non-boldface characters such as b denote scalars, lowercase bold-faced characters such as x denote vectors, uppercase bold-faced characters such as A denote matrices and calligraphic uppercase characters such as \({{{{{{{\mathcal{Z}}}}}}}}\) denote sets. We let [n] denote the set of indices {1, …, n}. We let e denote the vector of ones, 0 denote the vector of all zeros, and \({\mathbb{I}}\) denote the identity matrix. We let ∥x∥_p denote the p-norm of a vector x for p ≥ 1. We let \({\mathbb{R}}\) denote the real numbers, \({{{{{{{{\mathcal{S}}}}}}}}}^{n}\) denote the cone of n × n symmetric matrices, and \({{{{{{{{\mathcal{S}}}}}}}}}_{+}^{n}\) denote the cone of n × n positive semidefinite matrices.

We also use some notations specific to the sum-of-squares (SOS) optimization literature; see ref. ³² for an introduction to computational algebraic geometry and ref. ³⁴ for a general theory of sum-of-squares and convex algebraic optimization. Specifically, we let \({\mathbb{R}}{[{{{{{{{\boldsymbol{x}}}}}}}}]}_{n,2d}\) denote the ring of real polynomials in the n-tuple of variables \({{{{{{{\boldsymbol{x}}}}}}}}\in {{\mathbb{R}}}^{n}\) of degree 2d, \({P}_{n,2d}:=\{p\in {\mathbb{R}}{[{{{{{{{\boldsymbol{x}}}}}}}}]}_{n,2d}:p({{{{{{{\boldsymbol{x}}}}}}}})\ge 0\quad \forall {{{{{{{\boldsymbol{x}}}}}}}}\in {{\mathbb{R}}}^{n}\}\) denote the convex cone of non-negative polynomials in n variables of degree 2d, and

denote the cone of sum-of-squares polynomials in n variables of degree 2d, which can be optimized over via \((\begin{array}{l}n+d\\ d\end{array})\) dimensional semidefinite matrices (c.f. ref. ¹⁶) using interior point methods¹⁷. Note that Σ[x]_n,2d ⊆ P_n,2d, and the inclusion is strict unless n ≤ 2, 2d ≤ 2 or n = 3, 2d = 4⁴⁷. Nonetheless, Σ[x]_n,2d provides a high-quality approximation of P_n,2d, since each non-negative polynomial can be approximated (in the ℓ₁ norm of its coefficient vector) to any desired accuracy ϵ > 0 by a sequence of sum-of-squares⁶⁵. If the maximum degree d is unknown, we suppress the dependence on d in our notation.

To define a notion of distance between polynomials, we also use several functional norms. Let ∥ ⋅ ∥_p denote the ℓ_p norm of a vector. Let \({{{{{{{\boldsymbol{\mu }}}}}}}}\in {{\mathbb{N}}}^{n}\) be the vector (μ₁, …, μ_n) and x^μ stand for the monomial \({x}_{1}^{{\mu }_{1}}\ldots {x}_{n}^{{\mu }_{n}}\). Then, for a polynomial \(q\in {{\mathbb{R}}}[{{{{{{{\boldsymbol{x}}}}}}}}]_{n,2d}\) with the decomposition \(q({{{{{{{\boldsymbol{x}}}}}}}})={\sum}_{{{{{{{{\boldsymbol{\mu }}}}}}}}\in {{\mathbb{N}}}^{n}:\parallel {{{{{{{\boldsymbol{\mu }}}}}}}}{\parallel }_{1}\le 2d}{a}_{{{{{{{{\boldsymbol{\mu }}}}}}}}}{{{{{{{{\boldsymbol{x}}}}}}}}}^{{{{{{{{\boldsymbol{\mu }}}}}}}}}\), we let the notation \(\parallel {{{{{{{\boldsymbol{q}}}}}}}}{\parallel }_{p}={({\sum}_{{{{{{{{\boldsymbol{\mu }}}}}}}}\in {{\mathbb{N}}}^{n}:\parallel {{{{{{{\boldsymbol{\mu }}}}}}}}{\parallel }_{1}\le 2d}{\alpha }_{{{{{{{{\boldsymbol{\mu }}}}}}}}}^{p})}^{1/p}\) denote the coefficient norm of the polynomial,

Finally, to derive new laws of nature from existing ones, we repeatedly invoke a fundamental result from real algebraic geometry called the Positivstellensatz (see, e.g., ref. ⁶⁶). Various versions of the Positivstellensatz exist, with stronger versions holding under stronger assumptions see ref. ⁶⁷, for a review, and any reasonable version being a viable candidate for our approach. For simplicity, we invoke a compact version due to³³, which holds under some relatively mild assumptions but nonetheless lends itself to relatively tractable optimization problems:

Theorem 1

(Putinar’s Positivstellensatz³³, see also Theorem 5.1 of ref. ^16): Consider the basic (semi) algebraic sets

where \({g}_{i},{h}_{j}\in {\mathbb{R}}{[x]}_{n}\), and \({{{{{{{\mathcal{G}}}}}}}}\) satisfies the Archimedean property (see also ref. ³⁴, Chap. 6.4.4), i.e., there exists an R > 0 and α₀, …α_k ∈ Σ[x]_n such that \(R-{\sum}_{i=1}^{n}{x}_{i}^{2}={\alpha }_{0}({{{{{{{\boldsymbol{x}}}}}}}})+{\sum}_{i=1}^{k}{\alpha }_{i}({{{{{{{\boldsymbol{x}}}}}}}}){g}_{i}({{{{{{{\boldsymbol{x}}}}}}}})\).

Then, for any \(f\in {\mathbb{R}}{[x]}_{n,2d}\), the implication

holds if and only if there exist SOS polynomials α₀, …, α_k ∈ Σ[x]_n,2d, and real polynomials \({\beta }_{1},\ldots,{\beta }_{l}\in {\mathbb{R}}{[{{{{{{{\boldsymbol{x}}}}}}}}]}_{n,2d}\) such that

Note that strict polynomial inequalities of the form h_i(x) > 0 can be modeled by introducing an auxiliary variable τ and requiring that h_i(x)τ² − 1 = 0, and thus our focus on non-strict inequalities in Theorem 1 is without loss of generality see also ref. ³⁴.

Remarkably, the Positivstellensatz implies that if we set the degree of α_is to be zero, then polynomial laws consistent with a set of equality-constrained polynomials can be searched over via linear optimization. Indeed, this subset of laws is sufficiently expressive that, as we demonstrate in our numerical results, it allows us to recover Kepler’s third law and Einstein’s dilation law axiomatically. Moreover, the set of polynomial natural laws consistent with polynomial (in)equalities can be searched via semidefinite or sum-of-squares optimization.

Overall problem setting: combining theory and data

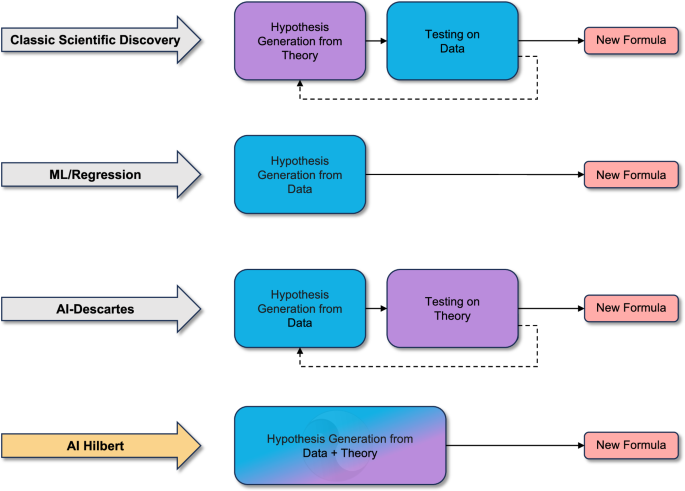
AI-Hilbert aims to discover an unknown polynomial model q(x) = 0, which contains one or more dependent variables raised to some power within the expression (to avoid the trivial solution q ≡ 0), is approximately consistent with our axioms \({{{{{{{\mathcal{G}}}}}}}}\) and \({{{{{{{\mathcal{H}}}}}}}}\) -meaning d^c is small, and explains our experimental data well, meaning \(q({\bar{{{{{{{{\boldsymbol{x}}}}}}}}}}_{i})\) is small for each data point i, and is of low complexity.

Let x₁, …, x_t denote the measurable variables, and let x₁ denote the dependent variable which we would like to ensure appears in our scientific law. Let \({{\Omega }}=\{{{{{{{{\boldsymbol{\mu }}}}}}}}\in {{\mathbb{N}}}^{n}:\parallel {{{{{{{\boldsymbol{\mu }}}}}}}}{\parallel }_{1}\le 2d\}\). Let the discovered polynomial expression by

where 2d is a bound on the maximum allowable degree of q. We formulate the following polynomial optimization problem:

where d^c, the distance between q and the background theory, is the optimal value of an inner minimization problem, λ > 0 is a hyperparameter that balances the relative importance of model fidelity to the data against model fidelity to a set of axioms, the first constraint ensures that x₁, our dependent variable, appears in q, the second constraint ensures that we do not include any unmeasured variables. In certain problem settings, we constrain d^c = 0, rather than penalizing the size of d^c in the objective.

Note that the formulation of the first constraint controls the complexity of the scientific discovery problem via the degree of the Positivstellensatz certificate: a smaller bound on the allowable degree in the certificate yields a more tractable optimization problem but a less expressive family of certificates to search over, which ultimately entails a trade-off that needs to be made by the user. Indeed, this trade-off has been formally characterized by Lasserre⁶⁵, who showed that every non-negative polynomial is approximable to any desired accuracy by a sequence of sum-of-squares polynomials, with a trade-off between the degree of the SOS polynomial and the quality of the approximation.

After solving Problem (10), one of two possibilities occurs. Either the distance between q and our background information is 0, or the Positivstellensatz provides a non-zero polynomial

which defines the discrepancy between our derived physical law and its projection onto our background information. In this sense, solving Problem (10) also provides information about the inverse problem of identifying a complete set of axioms that explain q. In either case, it follows from the Positivstellensatz that solving Problem (10) for different hyperparameter values and different bounds on the degree of q eventually yields polynomials that explain the experimental data well and are approximately derivable from background theory.

Discovering scientific laws from background theory alone

Suppose that the background theory \({{{{{{{\mathcal{B}}}}}}}}\) constitutes a complete set of axioms that fully describe our physical system. Then, any polynomial that contains our dependent variable x₁ and is derivable from our system of axioms is a valid physical law. Therefore, we need not even collect any experimental data, and we can solve the following feasibility problem to discover a valid law (let \({{\Omega }}=\{{{{{{{{\boldsymbol{\mu }}}}}}}}\in {{\mathbb{N}}}^{n}:\parallel {{{{{{{\boldsymbol{\mu }}}}}}}}{\parallel }_{1}\le 2d\}\)):

where the second and third constraints ensure that we include the dependent variable x₁ in our formula q and rule out the trivial solution q = 0, and exclude any solutions q that contain uninteresting symbolic variables respectively.

Note that if we do not have any inequality constraints in either problem, then we may often eliminate α_i and obtain a linear optimization problem.

Hagen-Poiseuille equation

We consider the problem of deriving the velocity of laminar fluid flow through a circular pipe, from a simplified version of the Navier-Stokes equations, an assumption that the velocity can be modeled by a degree-two polynomial in the radius of the pipe, and a no-slip boundary condition. Let u(r) denote the velocity in the pipe where r is the distance from the center of the pipe, R denotes the radius of the pipe, Δp denotes the pressure differential throughout the pipe, L denotes the length of the pipe, and μ denote the viscosity of the fluid, we have the following velocity profile for r ∈ [0, R]:

We now derive this law axiomatically by assuming that the velocity profile can be modeled by a symmetric polynomial and iteratively increasing the degree of the polynomial until we obtain a polynomial solution, consistent with Occam’s Razor. Accordingly, we initially set the degree of u to be two and add together the following terms with appropriate polynomial multipliers:

Here Equation (14) posits a quadratic velocity profile in r, Equation (15) imposes a simplified version of the Navier-Stokes equations in spherical coordinates, Equation (16) imposes a no-slip boundary condition on the velocity profile of the form u(R) = 0, and Equation (17) posits that the pressure gradient throughout the pipe is constant. The variables in this axiom system are u, r, R, L, μ, Δp, c₀, c₂, and \(\frac{dp}{dx}\). We treat \({c}_{0},{c}_{2},\frac{dp}{dx}\) as variables that cannot be measured and use the differentiate function in Julia to symbolically differentiate u = c₀ + c₂r² with respect to r in Equation (15) before solving the problem, giving the equivalent expression \(4{c}_{2}\mu r-r\frac{dp}{dx}\). Solving Problem (12) with u as the dependent variable, and searching for polynomial multipliers (and polynomial q) of degree at most 3 in each variable and an overall degree of at most 6, we get the expression:

which confirms the result. The associated polynomial multipliers for Equations (14)–(17) are:

Radiated gravitational wave power

We now consider the problem of deriving the power radiated from gravitational waves emitted by two-point masses orbiting their common center of gravity in a Keplerian orbit, as originally derived by Peters and Mathews⁶⁸ and verified for binary star systems by Hulse and Taylor⁶⁹. Specifically,⁶⁸ showed that the average power generated by such a system is:

where P is the (average) power of the wave, G = 6.6743 × 10⁻¹¹ m³ kg⁻¹ s⁻² is the universal gravitational constant, c is the speed of light, m₁, and m₂ are the masses of the objects, and we assume that the two objects orbit a constant distance of r away from each other. Note that this equation is one of the twenty so-called bonus laws considered in the work introducing AI-Feynman²², and notably, is one of only two such laws that neither AI-Feynman nor Eureqa⁷⁰ were able to derive. We now derive this law axiomatically, by combining the following axioms with appropriate multipliers:

where we make the variable substitution \(x=\cos \phi,y=\sin \phi\), \({{{{{{{\rm{Tr}}}}}}}}\) stands for the trace function, and we manually define the derivative of a bivariate degree-two trigonometric polynomial in ϕ = ϕ₀ + ωt in (x, y) in terms of (x, y, ω) as the following linear operator:

Note that Equation (24) is a restatement of Kepler’s previously derived third law of planetary motion, Equation (25) provides the gravitational power of a wave when the wavelength is large compared to the source dimensions, by linearizing the equations of general relativity, the third equation defines the quadruple moment tensor, and Equation (26) (which we state as x² + y² = 1 within our axioms) is a standard trigonometric identity. Solving Problem (12) with P as the dependent variable, and searching for a formula involving P, G, r, c, m₁, m₂ with polynomial multipliers of degree at most 20, and allowing each variable to be raised to power for the variables (P, x, y, ω, G, r, c, m₁, m₂) of at most (1, 4, 4, 4, 3, 6, 1, 5, 5) respectively, then yields the following equation:

which verifies the result. Note that this equation is somewhat expensive to derive, owing to the fact that searching over the set of degree 20 polynomial multipliers necessitates generating a large number of linear equalities, and writing these equalities to memory is both time and memory-intensive. Accordingly, we solved Problem (12) using the MIT SuperCloud environment⁷¹ with 640 GB RAM. The resulting system of linear inequalities involves 416392 candidate monomials, and takes 14368s to write the problem to memory and 6.58s to be solved by Mosek. This shows that the correctness of the universal gravitational wave equation can be confirmed via the following multipliers:

Finally, Fig. 4 illustrates how the Positivstellensatz derives this equation, by demonstrating that (setting m₁ = m₂ = c = G = 1), the gravitational wave equation is precisely the set of points (ω, r, P) where our axioms hold with equality.

Einstein’s Relativistic Time Dilation Law

Next, we consider the problem of deriving Einstein’s relativistic time dilation formula from a complete set of background knowledge axioms plus an inconsistent Newtonian axiom, which posits that light behaves like a mechanical object. We distinguish between these axioms using data on the relationship between the velocity of a light clock and the relative passage of time, as measured experimentally by Chou et al.⁷² and stated explicitly in the work of Cornelio et al.⁴³, Tab. 6.

Einstein’s law describes the relationship between how two observers in relative motion to each other observe time and demonstrates that observers moving at different speeds experience time differently. Indeed, letting the constant c denote the speed of light, the frequency f of a clock moving at a speed v is related to the frequency f₀ of a stationary clock via

We now derive this law axiomatically, by adding together the following five axioms with appropriate polynomial multipliers:

plus the following (inconsistent) Newtonian axiom:

where dt₀ denotes the time required for a light to travel between two stationary mirrors separated by a distance d, and dt denotes the time required for light to travel between two similar mirrors moving at velocity v, giving a distance between the mirrors of L.

These axioms have the following meaning: Equation (33) relates the time required for light to travel between two stationary mirrors to their distance, Equation (34) similarly relates the time required for light to travel between two mirrors in motion to the effective distance L, Equation (35) relates the physical distance between the mirrors d to their effective distance L induced by the motion v via the Pythagorean theorem, and Equations (36), (37) relate frequencies and periods. Finally, Equation (38) assumes (incorrectly) that light behaves like other mechanical objects, meaning if it is emitted orthogonally from an object traveling at velocity v, then it has velocity \(\sqrt{{v}^{2}+{c}^{2}}\).

By solving Problem (10) with a cardinality constraint c.f. refs. ^73,74 that we include at most τ = 5 axioms (corresponding to the exclusion of one axiom), a constraint that we must exclude either Equation (34) or Equation (38), f as the dependent variable, experimental data in f, f₀, v, c to separate the valid and invalid axioms (obtained from⁴³, Tab. 6 by setting f₀ = 1 to transform the data in (f − f₀)/f₀ into data in f, f₀), f₀, v, c as variables that we would like to appear in our polynomial formula \(q({{{{{{{\boldsymbol{x}}}}}}}})=0\,\forall {{{{{{{\boldsymbol{x}}}}}}}}\in {{{{{{{\mathcal{G}}}}}}}}\cap {{{{{{{\mathcal{H}}}}}}}}\), and searching the set of polynomial multipliers of degree at most 2 in each term, we obtain the law:

in 6.04 seconds using Gurobi version 9.5. 1. Moreover, we immediately recognize this as a restatement of Einstein’s law (32). This shows that the correctness of Einstein’s law can be verified by multiplying the (consistent relativistic set of) axioms by the following polynomials:

Moreover, it verifies that relativistic axioms, particularly the axiom cdt = 2L, fit the light clock data of ref. ⁷² better than Newtonian axioms, because, by the definition of Problem (10), AI-Hilbert selects the combination of τ = 5 axioms with the lowest discrepancy between the discovered scientific formula and the experimental data.

Kepler’s Third Law of Planetary Motion

We now consider the problem of deriving Kepler’s third law of planetary motion from a complete set of background knowledge axioms plus an incorrect candidate formula as an additional axiom, which is to be screened out using experimental data. To our knowledge, this paper is the first work that addresses this particularly challenging problem setting. Indeed, none of the approaches to scientific discovery reviewed in the introduction successfully distinguish between correct and incorrect axioms via experimental data by solving a single optimization problem. The primary motivation for this experiment is to demonstrate that AI-Hilbert provides a system for determining whether, given a background theory and experimental data, it is possible to improve upon a state-of-the-art scientific formula using background theory and experimental data.

Kepler’s law describes the relationship between the distance between two bodies, e.g., the sun and a planet, and their orbital periods and takes the form:

where G = 6.6743 × 10⁻¹¹ m³ kg⁻¹ s⁻² is the universal gravitational constant,m₁, and m₂ are the masses of the two bodies, d₁ and d₂ are the respective distances between m₁, m₂ and their common center of mass, and p is the orbital period. We now derive this law axiomatically by adding together the following five axioms with appropriate polynomial multipliers:

plus the following (incorrect) candidate formula (as an additional axiom) proposed by Cornelio et al.⁴³ for the exoplanet dataset (where the mass of the planets can be discarded as negligible when added to the much bigger mass of the star):

Here F_g and F_c denote the gravitational and centrifugal forces in the system, and w denotes the frequency of revolution. Note that we replaced p with 2πp in our definition of revolution period in order that π does not feature in our equations; we divide p by 2π after deriving Kepler’s law.

The above axioms have the following meaning: Equation (46) defines the center of mass of the dynamical system, Equation (47) defines the gravitational force of the system, Equation (48) defines the centrifugal force of the system, Equation (49) matches the centrifugal and dynamical forces, and Equation (50) relates the frequency and the period of revolution.

Accordingly, we solve our polynomial optimization problem under a sparsity constraint that at most τ = 5 axioms can be used to derive our model, a constraint that d^c = 0 (meaning we need not specify the hyperparameter λ in (10)), by minimizing the objective

where q is our implicit polynomial and \({\{\bar{{{{{{{{{\boldsymbol{x}}}}}}}}}_{i}}\}}_{i=1}^{4}\) is a set of observations of the revolution period of binary stars stated in ref. ⁴³, Tab. 5. Searching over the set of degree-five polynomials q derivable using degree six certificates then yields a mixed-integer linear optimization problem in 18958 continuous and 6 discrete variables, with the solution:

which is precisely Kepler’s third law. The validity of this equation can be verified by adding together our axioms with the weights:

as previously summarized in Fig. 3. This is significant, because existing works on symbolic regression and scientific discovery^22,75 often struggle to derive Kepler’s law, even given observational data. Indeed, our approach is also more scalable than deriving Kepler’s law manually; Johannes Kepler spent four years laboriously analyzing stellar data to arrive at his law⁷⁶.

Kepler’s law revisited with missing axioms

We now revisit the problem of deriving Kepler’s third law of planetary motion considered, with a view to verifying AI-Hilbert’s ability to discover scientific laws from a combination of theory and data. Specifically, rather than providing a complete (albeit inconsistent) set of background theories, we suppress a subset of the axioms (46)–(50) and investigate the number of noiseless data points required to recover Equation (53). To simplify our analysis, we set G = 1 and generate noiseless data observations by sampling the values of the independent variables (the masses of the two bodies and the distance between them) uniformly at random in the ranges observed in real data (i.e., exoplanet dataset in AI-Descartes⁴³) and computing the value of the dependent variable (the revolution period) using the ground truth formula.

To exploit the fact that our data observations are noiseless, we solve the following variant of (10):

where we set λ₁ = 0.9, λ₂ = 0.01, ϵ = 10⁻⁷ for all experiments, seek a degree 4 polynomial q using a proof certificate of degree at most 6, and use L₁-coefficient norm of q as a regularization term analogously to Lasso regression⁷⁷. Note that the second-to-last constraint ensures that the derived polynomial q explains all (noiseless) observations up to a small tolerance. Further, the last constraint is imposed as a linear inequality constraint with an auxiliary binary variable via the big-M technique^78,79, to ensure that the derived formula includes at least one term not involving the rotation period.

Figure 5 depicts the ℓ₂ coefficient distance between the scientific formula derived by AI-Hilbert and Equation (53) mod d₁m₁ − d₂m₂ = 0 as we increase the number of data points, where we suppress the axiom d₁m₁ − d₂m₂ = 0 (left), where we suppress all axioms (right). In both cases, there is an all-or-nothing phase transition [(c.f. ref. ⁸⁰), for a discussion of this phenomenon throughout machine learning] in AI-Hilbert’s ability to recover the scientific law, where before a threshold number of data points, AI-Hilbert cannot recover Kepler’s law, and beyond the threshold, AI-Hilbert recovers the law exactly.

Note that the increase in the coefficient distance before m = 71 data points reflects that solutions near q = 0 (and thus closer in coefficient norm to the ground truth) are optimal with m = 0 data points but do not fit a small number of data points perfectly, while polynomials q further from the ground truth in coefficient norm fit a small number of data points perfectly. Indeed, the total error with respect to the training data is less than 10⁻⁵ for all values of m in both problem settings.

Figure 5 reveals that when only the axiom d₁m₁ − d₂m₂ = 0 is missing, it is possible to perform scientific discovery with as few as 46 data points, while at least 71 data points are needed when all axioms are missing. This is because the axiom d₁m₁ − d₂m₂ = 0 multiplied by the term in the proof certificate \(-{d}_{2}^{2}{p}^{2}{w}^{2}\) is of a similar complexity as Kepler’s Third Law. Thus, the value of d₁m₁ − d₂m₂ = 0 is 46 data points, while the value of all axioms is 71 data points. The value of data compared to background theory depends, in general, on the problem setting and the data quality, as well as how well dispersed the data samples are.

Bell inequalities

We now consider the problem of deriving Bell Inequalities in quantum mechanics. Bell Inequalities⁸¹ are well-known in physics because they provide bounds on the correlation of measurements in any multi-particle system which obeys local realism (i.e., for which a joint probability distribution exists), that are violated experimentally, thus demonstrating that the natural world does not obey local realism. For ease of exposition, we prove a version called the GHZ inequality⁸². Namely, given random variables A, B, C which take values on { ± 1}, for any joint probability distribution describing A, B, C, it follows that

but this bound is violated experimentally⁸³.

We derive this result axiomatically, using Kolmogorov’s probability axioms. In particular, letting \({p}_{-1,1,-1}={\mathbb{P}}(A=-1,B=1,C=-1)\), deriving the largest lower bound for which this inequality holds is equivalent to solving the following linear optimization problem:

where \({{{{{{{\mathcal{S}}}}}}}}:=\{{{{{{{{\boldsymbol{p}}}}}}}}\ge {{{{{{{\boldsymbol{0}}}}}}}},{{{{{{{{\boldsymbol{e}}}}}}}}}^{\top }{{{{{{{\boldsymbol{p}}}}}}}}=1\}\), p_AB ≔ p_{−1,−1,−1} + p_−1,−1,1 + p_1,1,−1 + p_1,1,1 and p_AC, p_BC are defined similarly.

We solve this problem using Gurobi and Julia, which verifies that γ = 1 is the largest value for which this inequality holds, and obtains the desired inequality. Moreover, the solution to its dual problem yields the certificate 2p_{−1,−1,−1} + 2p_1,1,1≥ 0, which verifies that 1 is indeed a valid lower bound for p_AB + p_BC + p_AC, by adding e^⊤p to the left-hand side of this certificate and 1 to the right-hand side.

To further demonstrate the generality and utility of our approach, we now derive a more challenging Bell inequality, namely the so-called I3322 inequality (c.f. ref. ⁸⁴). Given particles A₁, A₂, A₃, B₁, B₂, B₃ which take values on { ± 1}, the inequality reveals that for any joint probability distribution, we have:

Using the same approach as previously, and defining p to be an arbitrary discrete probability measure on {± 1}⁶, we verify that the smallest such upper bound which holds for each joint probability measure is 4, with the following polynomial certificate modulo e^⊤p = 1:

where an index of 1 denotes that a random variable took the value − 1 and an index of 2 denotes that a random variable took the value 1, and the random variables are indexed in the order A₁, A₂, A₃, B₁, B₂, B₃.